绪论 单元测试
1、判断题:
复变函数论与运算微积这门课主要讨论复变函数与积分变换的基本理论和方法。可以用来解决诸如流体力学、电磁学、电子工程及通讯等问题的有力工具,并且在微分方程、概率论及数论等数学的其他分支中都有着广泛的应用。( )
选项:
A:错
B:对
答案: 【对】
第一章 单元测试
1、单选题:
复数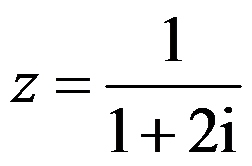 的辐角是( )。
的辐角是( )。
选项:
A: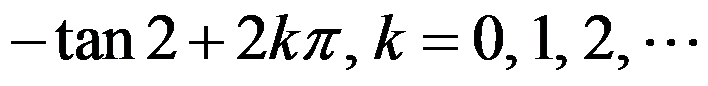
B: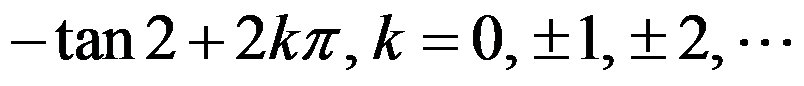
C:
D: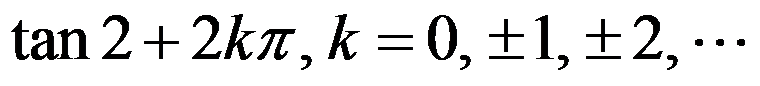
答案: 【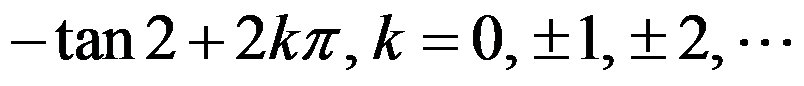
】
2、单选题:
若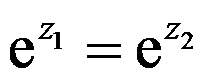 ,则( )。
,则( )。
选项:
A: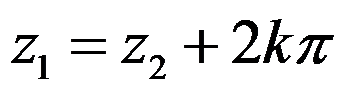 ,
,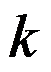 为任意整数
为任意整数
B: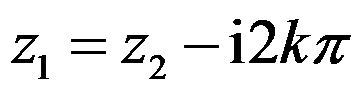 ,
,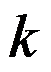 为任意整数
为任意整数
C: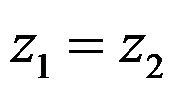
D: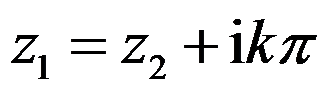 ,
,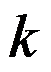 为任意整数
为任意整数
答案: 【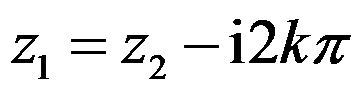 ,
,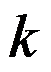 为任意整数
为任意整数
】
3、单选题:
下列集合中,有界的单连通区域是( )。
选项:
A: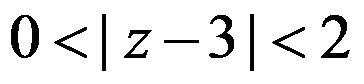
B: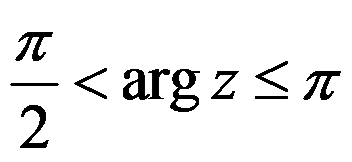
C: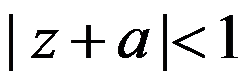
D: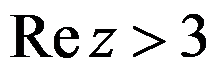
答案: 【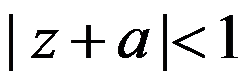
】
4、单选题:
设复数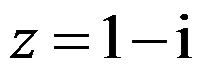 ,则
,则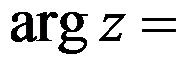 ( )。
( )。
选项:
A: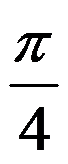
B: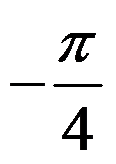
C: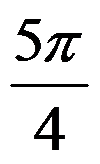
D: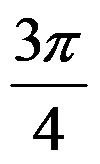
答案: 【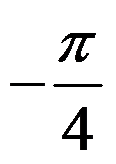
】
5、单选题:
设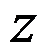 为非零复数,
为非零复数,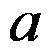 ,
,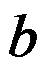 为实数且
为实数且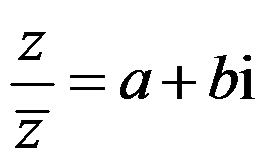 ,则
,则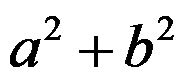 ( )。
( )。
选项:
A:等于1
B:等于0
C:大于1
D:小于1
答案: 【等于1】
第二章 单元测试
1、单选题:
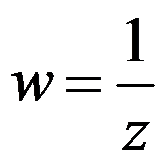 将
将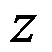 平面上的曲线
平面上的曲线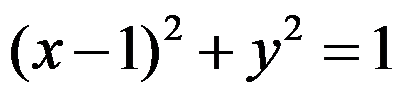 映射成
映射成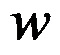 平面上的曲线( )。
平面上的曲线( )。
选项:
A: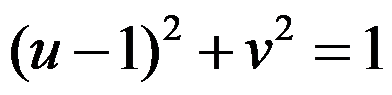
B: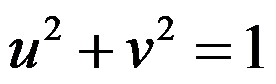
C: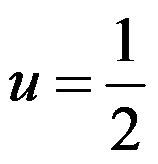
D: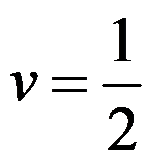
答案: 【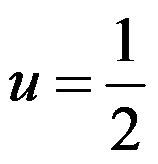
】
2、单选题:
以坐标原点为中心,焦点在实轴上,长半轴为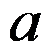 ,短半轴为
,短半轴为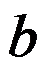 的椭圆周的复参数方程为( )。
的椭圆周的复参数方程为( )。
选项:
A: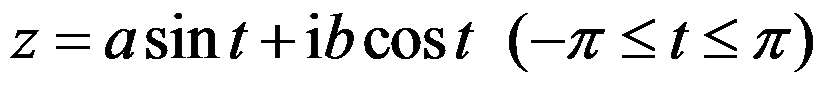
B: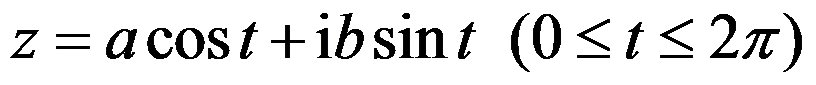
C: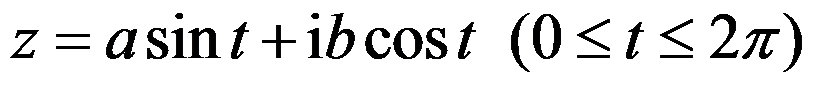
D: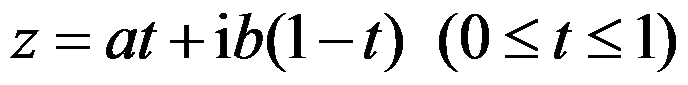
答案: 【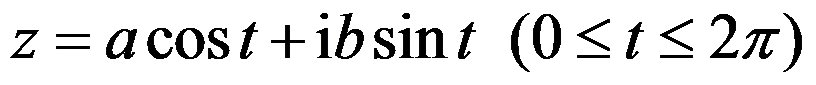
】
3、单选题:
下列函数中,在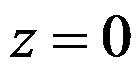 处不连续的是( )。
处不连续的是( )。
选项:
A: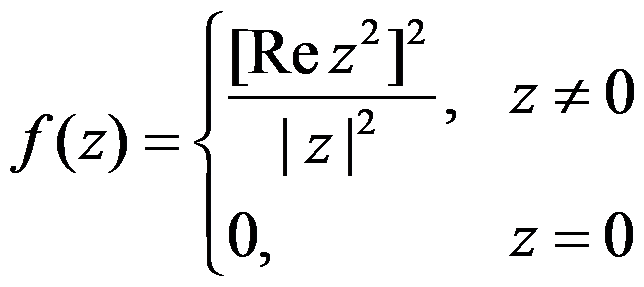
B: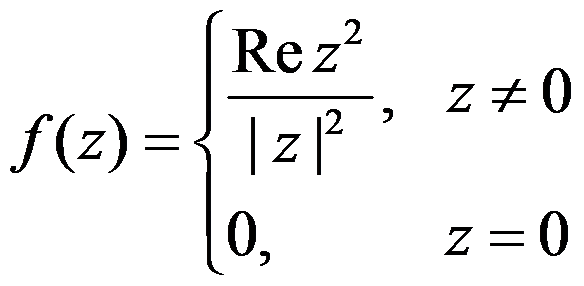
C: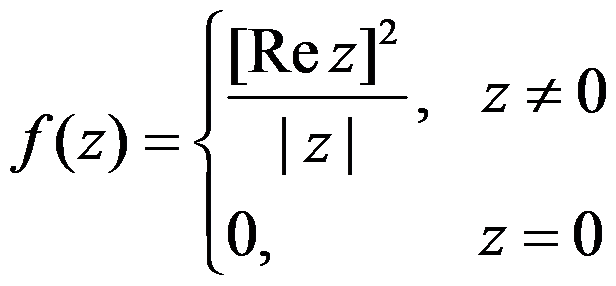
D: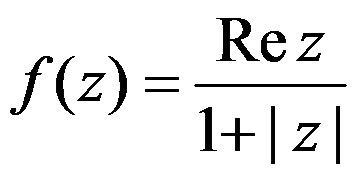
答案: 【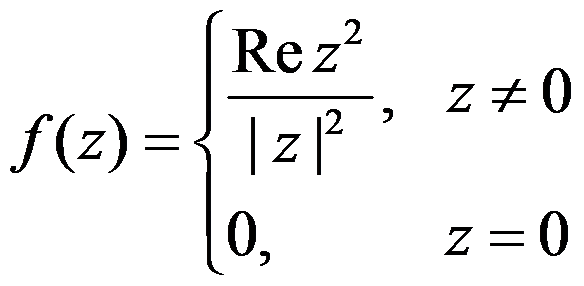
】
4、单选题:
函数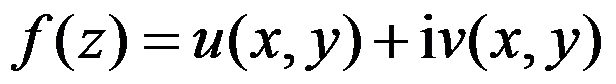 在点
在点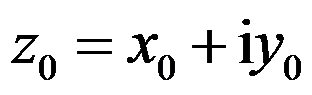 处连续的充要条件是( )。
处连续的充要条件是( )。
选项:
A: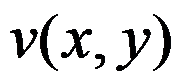 在点
在点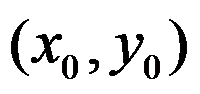 处连续
处连续
B: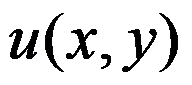 和
和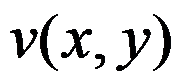 在点
在点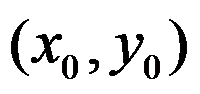 处均连续
处均连续
C: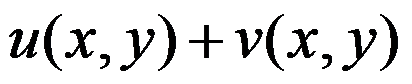 在点
在点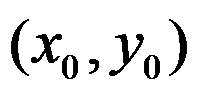 处连续
处连续
D: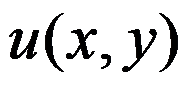 在点
在点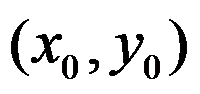 处连续
处连续
答案: 【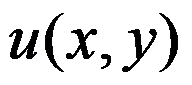 和
和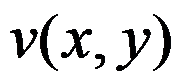 在点
在点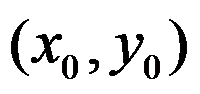 处均连续
处均连续
】
5、单选题:
极限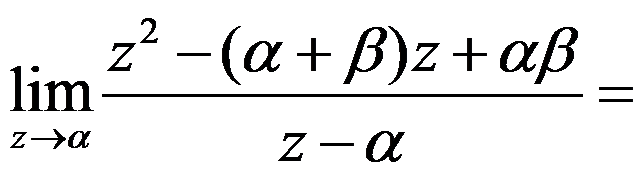 ( )。
( )。
选项:
A: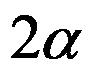
B: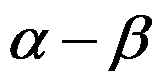
C: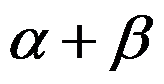
D:不存在
答案: 【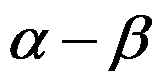
】
第三章 单元测试
1、单选题:
函数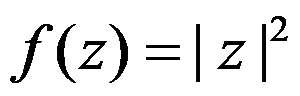 在复平面上( )。
在复平面上( )。
选项:
A:处处连续,且在点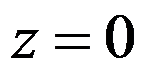 处解析
处解析
B:处处连续,且在点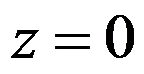 处可导
处可导
C:处处连续,处处不可导
D:处处不连续
答案: 【处处连续,且在点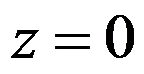 处可导
处可导
】
2、单选题:
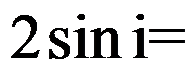 ( )。
( )。
选项:
A: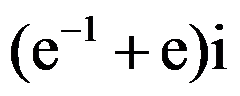
B: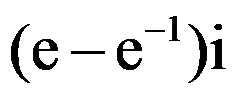
C: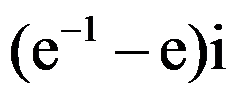
D: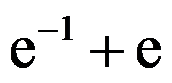
答案: 【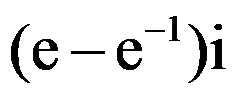
】
3、单选题:
在复平面上,下列命题中不正确的是( )。
选项:
A: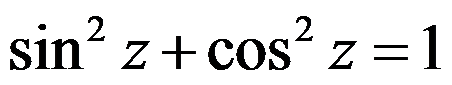
B: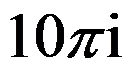 是
是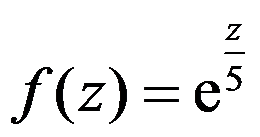 的周期
的周期
C: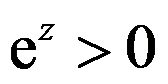
D: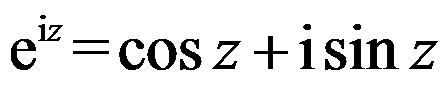
答案: 【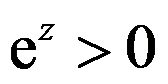
】
4、单选题:
设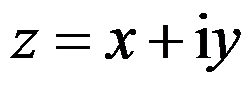 ,则下列函数为解析函数的是( )。
,则下列函数为解析函数的是( )。
选项:
A: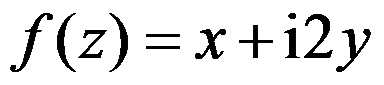
B: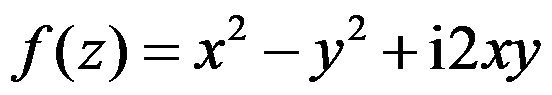
C: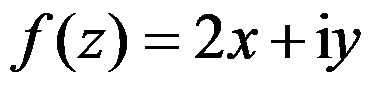
D: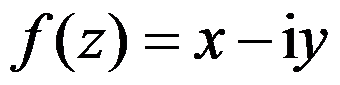
答案: 【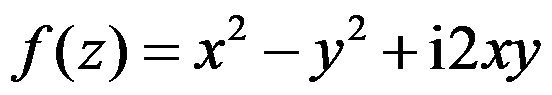
】
5、单选题:
已知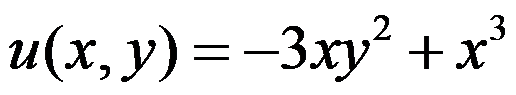 为调和函数,则满足
为调和函数,则满足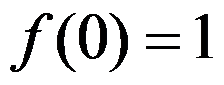 的解析函数
的解析函数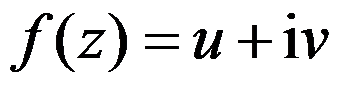 为( )。
为( )。
选项:
A: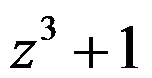
B: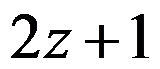
C: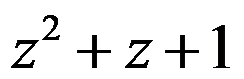
D: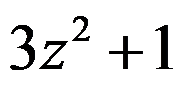
答案: 【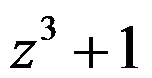
】
第四章 单元测试
1、单选题:
设曲线 为单位圆
为单位圆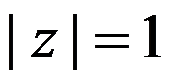 ,取正向,则积分
,取正向,则积分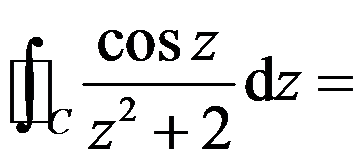 ( )。
( )。
选项:
A: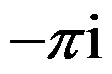
B: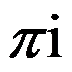
C:
D: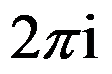
答案: 【
】
2、单选题:
设 为正向圆周
为正向圆周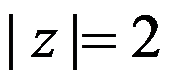 ,则
,则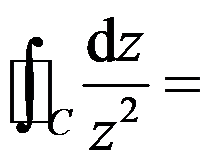 ( )。
( )。
选项:
A: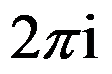
B:
C: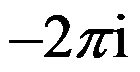
D: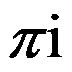
答案: 【
】
3、单选题:
设 是绕点
是绕点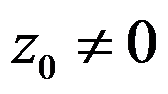 的正向简单闭曲线,则
的正向简单闭曲线,则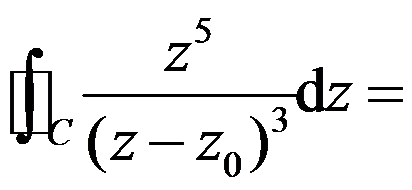 ( )。
( )。
选项:
A: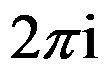
B:
C: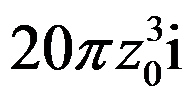
D: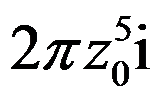
答案: 【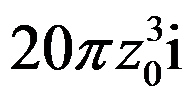
】
4、单选题:
设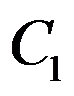 ,
,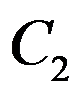 分别是正向圆周
分别是正向圆周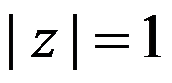 与
与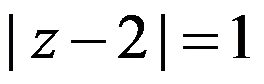 ,则
,则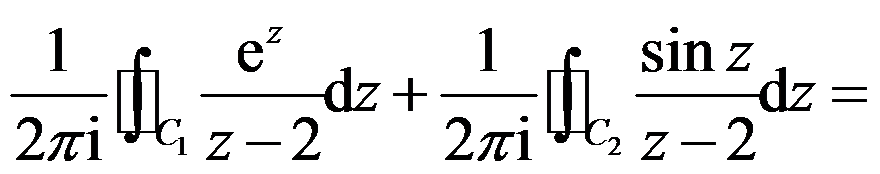 ( )。
( )。
选项:
A: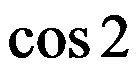
B:
C: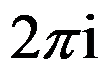
D: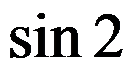
答案: 【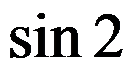
】
5、单选题:
积分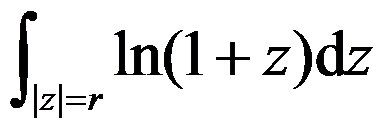
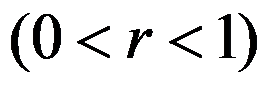 等于( )。
等于( )。
选项:
A: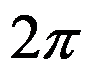
B:
C: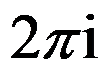
D:
答案: 【
】
第五章 单元测试
1、单选题:
如果幂级数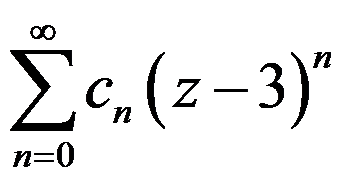 在点
在点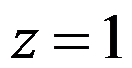 处收敛,则该级数必在( )。
处收敛,则该级数必在( )。
选项:
A:点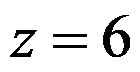 处发散
处发散
B:点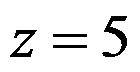 处收敛
处收敛
C:点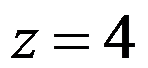 处条件收敛
处条件收敛
D:点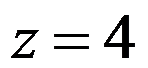 处绝对收敛
处绝对收敛
答案: 【点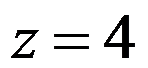 处绝对收敛
处绝对收敛
】
2、单选题:
函数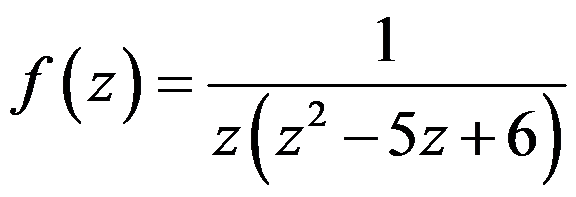 在区域( )内不能展开成罗朗级数。
在区域( )内不能展开成罗朗级数。
选项:
A: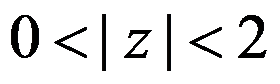
B: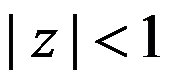
C: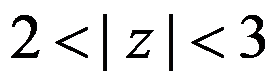
D: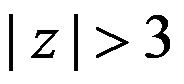
答案: 【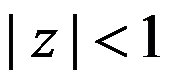
】
3、单选题:
幂级数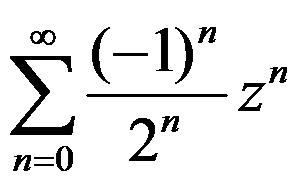 的收敛半径为( )。
的收敛半径为( )。
选项:
A:
B: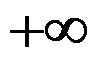
C:
D: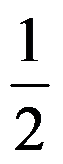
答案: 【
】
4、单选题:
下列命题中假命题的是( )。
选项:
A:级数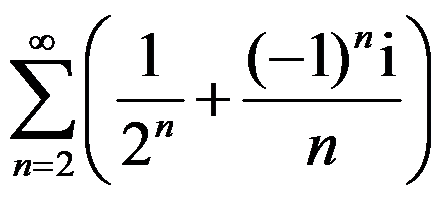 是条件收敛的
是条件收敛的
B:级数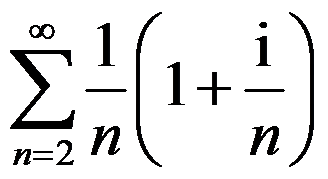 是收敛的
是收敛的
C:级数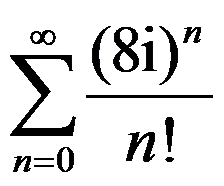 是绝对收敛的
是绝对收敛的
D:级数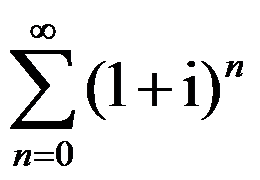 是发散的
是发散的
答案: 【级数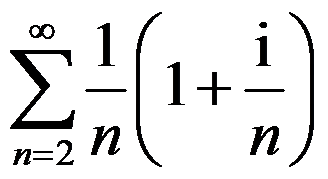 是收敛的
是收敛的
】
5、单选题:
函数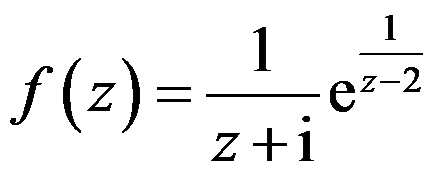 在
在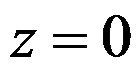 处的泰勒展式的收敛半径为( )。
处的泰勒展式的收敛半径为( )。
选项:
A:无法确定
B:
C:
D: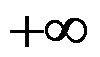
答案: 【
】

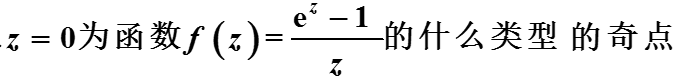 ( )。
( )。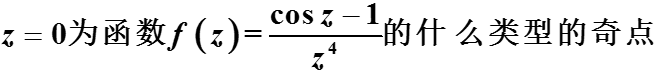 ( )。
( )。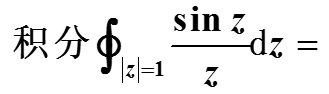 ( )。
( )。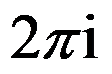
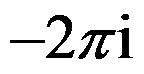


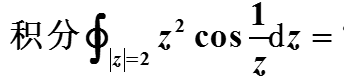 ( )。
( )。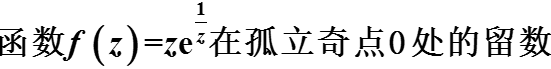 ( )。
( )。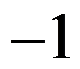
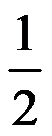
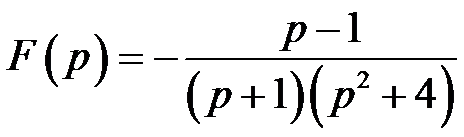 的Laplace逆变换为( )。
的Laplace逆变换为( )。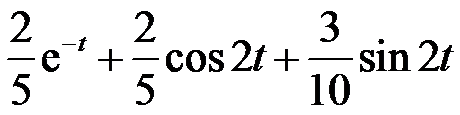
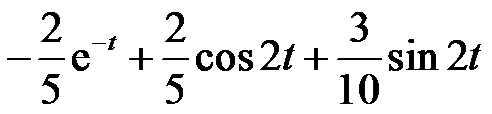
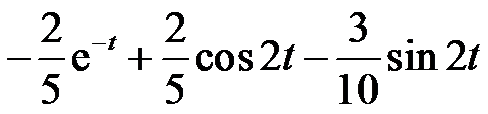
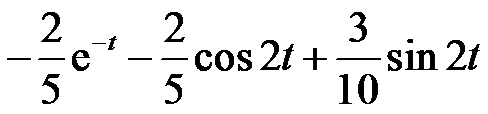
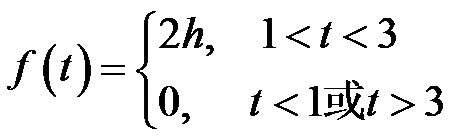 的laplace变换为 ( )。
的laplace变换为 ( )。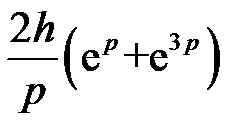
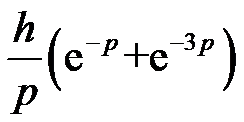
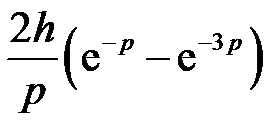
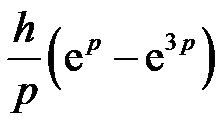
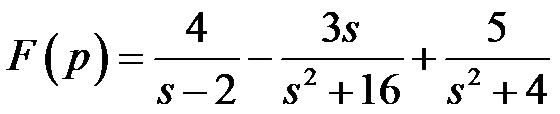 的Laplace逆变换为 ( )。
的Laplace逆变换为 ( )。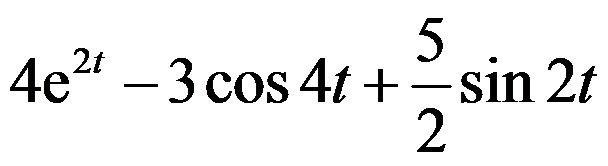
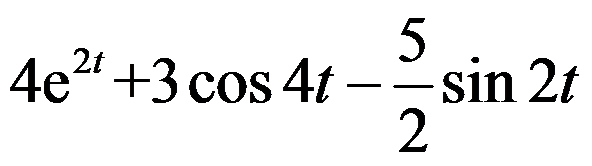
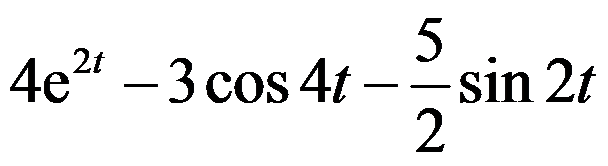
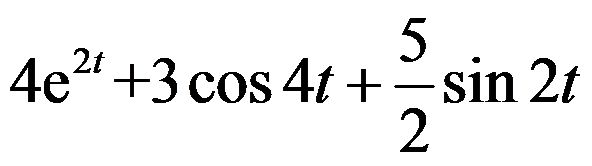
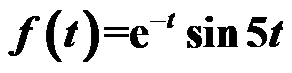 的Laplace变换为( )
的Laplace变换为( )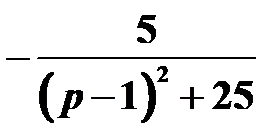
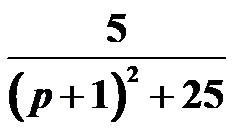
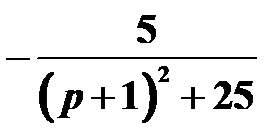
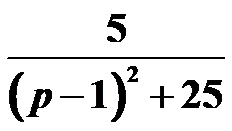
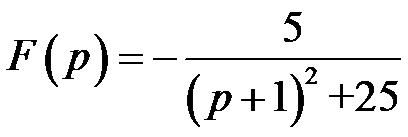 的Laplace逆变换为( )。
的Laplace逆变换为( )。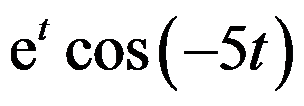
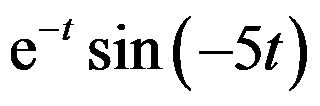
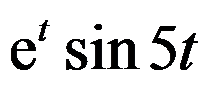
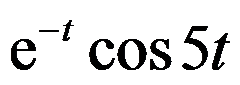







评论0