第一章 单元测试
1、判断题：
When the error propagation formula is 
, it is called exponential error propagation. ( )
选项：
A:对
B:错
答案: 【错】
2、单选题：
When performing（ ）operation with two similar numbers, it is easy to cause larger errors.（
选项：
A:Subtraction
B:Addition
C:Multiplication
D:Division
答案: 【Subtraction】
3、多选题：
Which problems should be solved by numerical analytical tool ( )?
选项：
A: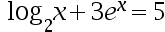
B: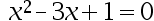
C: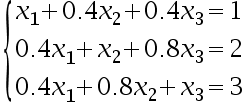
D: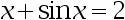
答案: 【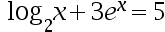
;
】
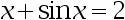
4、单选题：
If p* =10.001 is an approximate of p = 10.000, then the relative error is ( )
选项：
A: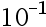
B: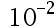
C: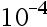
D: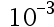
答案: 【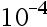
】
5、单选题：
To approach 1/3, we should use at least ( ) significant digits to guarantee a relative error of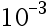 
选项：
A: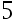
B: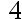
C: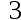
D: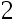
答案: 【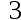
】
第二章 单元测试
1、判断题：
Suppose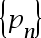 
is a sequence that converges to p, with 
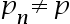for all n. If positive constants 
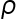and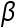 
exist with
.
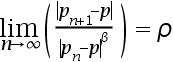Then, if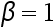 
, the sequence is linearly convergent. ( )
选项：
A:错
B:对
答案: 【对】
2、单选题：
The convergence rate of the bisection method is（ ）.
选项：
A: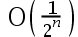
B: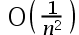
C: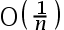
D: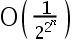
答案: 【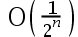
】
3、单选题：
The convergence rate of the Newton’s method is（ ）.
选项：
A: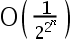
B: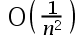
C: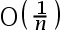
D: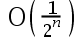
答案: 【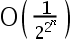
】
4、判断题：
Let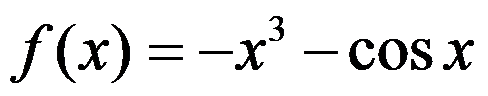 
and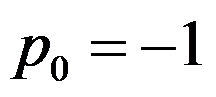 
. Use Newton’s method to find 
. 
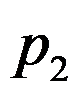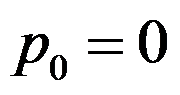can be used as an initial point? （ ）
选项：
A:对
B:错
答案: 【错】
5、判断题：
The fixed-point problem g(x)=x-x3-4×2+10 cannot converge for initial point x0=1.5. （ ）
选项：
A:错
B:对
答案: 【对】
第三章 单元测试
1、判断题：
If a vector sequence converges to X in the L1 norm, it also converges to X in the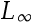 
norm.（ ）
选项：
A:错
B:对
答案: 【对】
2、判断题：
A sufficient condition for the existence of a unique fixed point is within a given interval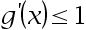 
.（ ）
选项：
A:错
B:对
答案: 【错】
3、判断题：
When the initial value is incorrectly selected, both fixed-point iteration and Newton’s method will fail to converge.（ ）
选项：
A:对
B:错
答案: 【对】
4、判断题：
Beginning with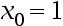 
, the second iteration of Newton’s method for the equation 
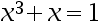is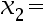 
0.6860. ( )
选项：
A:对
B:错
答案: 【对】
5、单选题：
The convergence rate of the fixed-point iterative method is（ ）.
选项：
A: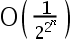
B: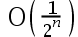
C: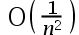
D: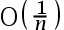
答案: 【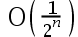
】
第四章 单元测试
1、判断题：
If A is symmetric, then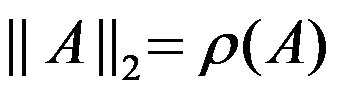 
. （ ）
选项：
A:错
B:对
答案: 【对】
2、判断题：
Given the linear system
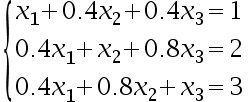
The Gauss-Seidel algorithm can be used to solve the system. ( )
选项：
A:对
B:错
答案: 【对】
3、判断题：
If the spectral radius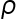 
of a matrix A satisfies 
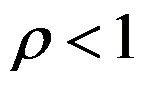, then A is a convergent matrix. ( )
选项：
A:对
B:错
答案: 【对】
4、多选题：
The iterative calculation formula for linear problems is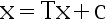 
, the iterative process can converge when T satisfies which of the following conditions?（ ）
选项：
A:n is large enough, the L1 norm of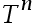 
is small enough
B:T is a convergent matrix
C:The spectral radius of T is less than 1.
D:n is large enough, the L2 norm of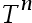 
is small enough
答案: 【n is large enough, the L1 norm of 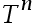is small enough
;
T is a convergent matrix
;
The spectral radius of T is less than 1.
;
n is large enough, the L2 norm of 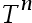is small enough
】
5、判断题：
For the iterative solution of linear problems, the Jacobi algorithm always converge faster than the Gauss-Seidel algorithm.（ ）
选项：
A:对
B:错
答案: 【错】
第五章 单元测试
1、判断题：
Passing n points, a polynomial with degree no more than n that satisfies the interpolation conditions exists and is unique.（ ）
选项：
A:错
B:对
答案: 【错】
2、多选题：
Which of the following statements are correct about polynomial fitting?（ ）
选项：
A:One of the advantages of polynomial fitting is that the algebraic operations of polynomials are still polynomials
B:The polynomial with the highest degree n-1 which pass through n given points is unique
C:Taylor polynomials can only approximate a function at a certain point
D:In a closed interval, there is no polynomial function to approximate the exponential function with sufficient precision
答案: 【One of the advantages of polynomial fitting is that the algebraic operations of polynomials are still polynomials;
The polynomial with the highest degree n-1 which pass through n given points is unique;
Taylor polynomials can only approximate a function at a certain point】
3、判断题：
Let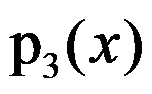 
be the interpolation polynomial for the data(0,0),(0.5,y),(1,3),and(2,2).The coefficient of 
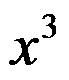in 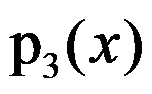is 6. Then y = 4.25. ( )
选项：
A:错
B:对
答案: 【对】
4、判断题：
Construct the Lagrange interpolating polynomial of degree 2 for the given values of x and y:
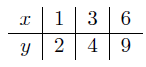
Then y =6.712 when x = 4.8. ( )
选项：
A:对
B:错
答案: 【对】
5、判断题：
Write the linear Lagrange interpolating polynomial that passes through the points (2; 4) and (5; 1). Then f(7)={2}. ( )
选项：
A:错
B:对
答案: 【错】
6、单选题：
The goal of least squares approximation minimizes the （ ） norm of the error.()
选项：
A: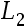
B: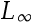
C: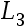
D: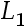
答案: 【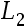
】
第六章 单元测试
1、单选题：
The error of the three-point numerical differentiation method is（ ）。
选项：
A: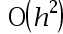
B: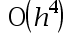
C: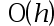
D: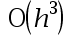
答案: 【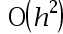
】
2、判断题：
When considering the rounding error, both the five-point and three-point numerical differentiation methods have the same optimal step length h. ( )
选项：
A:对
B:错
答案: 【错】
3、单选题：
The error of the five-point numerical differentiation method is（ ）。
选项：
A: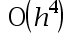
B: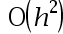
C: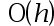
D: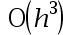
答案: 【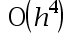
】
4、判断题：
When considering the rounding error, the larger the h, the higher the precision of the numerical differentiation.（ ）
选项：
A:错
B:对
答案: 【错】
5、判断题：
Using Richardson’s extrapolation method, low-order formulas can be used to derive high-order formulas for solving numerical differentials. （ ）
选项：
A:对
B:错
答案: 【对】
第七章 单元测试
1、单选题：
The error order of the trapezoidal integral formula is（ ）。
选项：
A: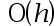
B: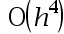
C: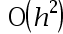
D: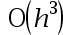
答案: 【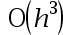
】
2、单选题：
The error order of the composite trapezoidal integral formula is（ ）.
选项：
A: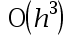
B: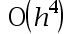
C: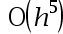
D: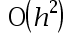
答案: 【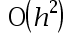
】
3、判断题：
The Simpson’s rule has a degree of precision 2. ( )
选项：
A:对
B:错
答案: 【错】
4、判断题：
Romberg integral is the application of Richardson extrapolation in numerical integration. ( )
选项：
A:对
B:错
答案: 【对】
5、判断题：
The quadrature formula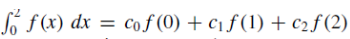 
is exact for all polynomials of degree less than or equal to 2. Then, c0=1/3, c1=4/3, c2=1/3. ( )
选项：
A:错
B:对
答案: 【对】
第八章 单元测试
1、多选题：
Which of the following functions are not Lipschitz continuous on [0,1]?（ ）。
选项：
A: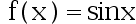
B: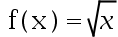
C: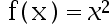
D: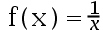
答案: 【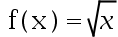
;
】
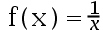
2、单选题：
The local truncation error of Euler’s method is（ ）.
选项：
A: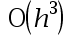
B: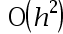
C: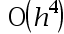
D: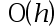
答案: 【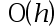
】
3、单选题：
The local truncation error of Runge-Kutta order 4 method is（ ）.
选项：
A: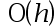
B: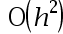
C: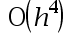
D: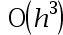
答案: 【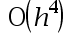
】
4、多选题：
What are the conditions for the existence of a unique solution for the boundary value problem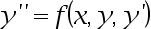 
?
()
选项：
A: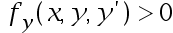
B: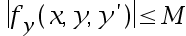
C: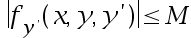
D: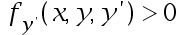
答案: 【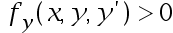
;
】
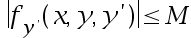
5、判断题：
The local truncation error of Heun ‘s method is {O(h3)}. ( )
选项：
A:错
B:对
答案: 【对】
评论0